[Cheng의 전자기학] 가우스의 법칙

 

 

1. 정전기장의 기본 가정

 

자유공간 내 정전하가 존재한다고 가정한다면, 전기장 세기 E만 고려한다.

 

$$\mathbf{\text{E}}=\underset{q\to 0}{lim}\frac{\mathbf{\text{F}}}{q}[V/m]$$

 

수식은 전기장 세기로, 전기장이 존재하는 공간에 매우 작은 시험전하가 존재할 때 이 전하가 받게 되는 힘의 크기를 단위전하당 비율로 정의한 값이다.

 

정전기장의 기본 가정은 다음과 같다.

 

$$\mathrm{\nabla }\cdot \mathbf{\text{E}}=\frac{\rho }{{ϵ}_0}$$

$$\mathrm{\nabla }\times \mathbf{\text{E}}=0$$

 

$\rho$는 자유전하의 부피밀도, ${ϵ}_0$는 자유공간에서의 유전율이다. 첫 번째 수식은 솔레노이드성이 아님을 의미하고 두 번째 수식은 비회전성을 의미한다. 두 수식을 적분형으로 나타내면 다음과 같다.

 

$${\int }_V\mathrm{\nabla }\cdot \mathbf{\text{E}}dv=\frac{1}{{ϵ}_0}{\int }_V\rho dv={\oint }_S\mathbf{\text{E}}\cdot d\mathbf{\text{s}}=\frac{Q}{{ϵ}_0}$$

$${\int }_S(\mathrm{\nabla }\times \mathbf{\text{E}})\cdot d\mathbf{\text{s}}={\oint }_C\mathbf{\text{E}}\cdot d\mathbf{\text{l}}=0$$

 

첫 번째 수식은 발산 정리를 사용하여 구할 수 있고 가우스의 법칙이라고 한다. 자유공간 내 어떤 닫힌 공간에서 바깥으로 발산되는 전기장 세기의 합이 그 공간 내부의 총전하량을 유전상수로 나눈 값으로 정의할 수 있다.

 

두 번째 수식은 스토크스 정리를 적용하여 얻을 수 있고 어떤 면 주위에 따라 폐곡선에 대한 전기장 세기의 선적분은 면 특성과 관계없이 항상 0 임을 나타낸다. 이 의미는 키르히호프의 전압 법칙과 같은 의미이다.

 

 

2. 쿨롱의 법칙

 

자유공간에 점전하 q가 정지된 경우, 전하 q 중심으로 반지름이 R인 가상 구면을 만든다. 구좌표계를 이용하여 가우스의 법칙을 적용해보면 다음과 같다.

 

$${\oint }_S\mathbf{\text{E}}\cdot d\mathbf{\text{s}}={\oint }_S({\mathbf{\text{a}}}_R{E}_R){\mathbf{\text{a}}}_{R}ds=E_R{\oint }_{S}ds=E_R(4\pi R^2)=\frac{q}{{ϵ}_0}$$

 

수식은 하나의 점전하에 의해 발생된 전기장 세기는 거리에 반비례하고, 점전하에 멀어지는 방사 방향으로 퍼짐을 의미한다.

 

서로 다른 n개의 독립 전하가 그룹을 형성하여 정전기장을 만들고 있다면 총 전기장 세기 E는 다음과 같다.

 

$$\mathbf{\text{E}}=\frac{1}{4\pi {ϵ}_0}\sum _{k=1}^n\frac{q_k(\mathbf{\text{R}}-{\mathbf{\text{R}}}_k^{\prime })}{|\mathbf{\text{R}}-{\mathbf{\text{R}}}_k^{\prime }{|}^3}(V/m)$$

 

만약 서로 다른 두 전하만 존재하는 경우는 다음처럼 나타낼 수 있다.

 

$$\mathbf{\text{E}}=\frac{p}{4\pi {ϵ}_0{R}^3}({\mathbf{\text{a}}}_{R}2\cos \theta +{\mathbf{\text{a}}}_{\theta }\sin \theta )(V/m)$$

 

$\mathbf{\text{p}}=q\mathbf{\text{d}}$로 p는 전기 쌍극자 모멘트를 의미하고 d는 -q에서 q로 향하는 벡터이다.

 

쌍극자의 전기장

 

전하가 연속적으로 분포한다면 전기장 세기는 다음처럼 표현할 수 있다.

 

$$\mathbf{\text{E}}=\frac{1}{4\pi {ϵ}_0}{\int }_{V^{\prime }}{\mathbf{\text{a}}}_R\frac{\rho }{R^2}d{v}^{\prime }$$

$$\mathbf{\text{E}}=\frac{1}{4\pi {ϵ}_0}{\int }_{S^{\prime }}{\mathbf{\text{a}}}_R\frac{{\rho }_s}{R^2}d{s}^{\prime }$$

$$\mathbf{\text{E}}=\frac{1}{4\pi {ϵ}_0}{\int }_{L^{\prime }}{\mathbf{\text{a}}}_R\frac{{\rho }_l}{R^2}d{l}^{\prime }$$

 

${\mathbf{\text{a}}}_R=\mathbf{\text{R}}/R$, ${\rho }_s$는 면전하밀도, ${\rho }_l$는 선전하밀도이다.

 

 

3. 가우스의 법칙

 

가우스의 법칙은 대칭적인 구조로 분포된 전하가 존재하는 경우 전기장의 세기를 구할 때 사용하며, 전기장 세기의 수직 성분이 상수값이 되는 폐곡면을 적절하게 선택해야 한다.

 

 

1. 무한히 긴 선전하에 의해 발생되는 전기장 세기

 

무한히 긴 선전하에 의해 발생되는 전기장은 방사형이고, 선전하에 수직 방향이다.

 

$${\oint }_S\mathbf{\text{E}}\cdot d\mathbf{\text{s}}={\int }_0^L{\int }_0^{2\pi }{E}_{r}rd\varphi dz=E_{r}r(2\pi )L=\frac{{\rho }_{l}L}{{ϵ}_0}$$

$$\mathbf{\text{E}}={\mathbf{\text{a}}}_r{E}_r={\mathbf{\text{a}}}_r\frac{{\rho }_l}{2\pi {ϵ}_{0}r}$$

가우스의 법칙 적용

 

2. 무한 판전하에 의해 발생하는 전기장 세기

 

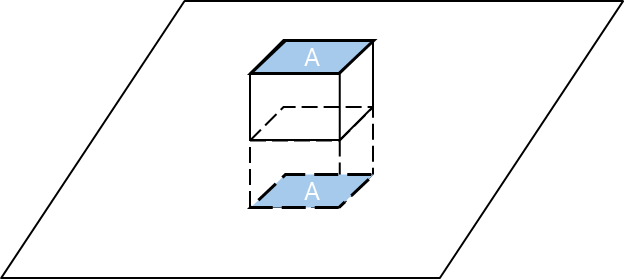
무한 판전하에 의해 발생하는 전기장은 판의 수직 방향으로 발생한다. 판전하를 중심으로 면적이 A인 직육면체 상자를 놓으면 직육면체의 윗면과 아랫면을 가우스 표면으로 설정할 수 있다. 직육면체의 측면은 전기장 세기와 방향이 수직이므로 고려하지 않아도 된다.

 

윗면 : $\mathbf{\text{E}}\cdot d\mathbf{\text{s}}=({\mathbf{\text{a}}}_z{E}_z)\cdot ({\mathbf{\text{a}}}_{z}ds)=E_{z}ds$

아랫면 : $\mathbf{\text{E}}\cdot d\mathbf{\text{s}}=(-{\mathbf{\text{a}}}_z{E}_z)\cdot (-{\mathbf{\text{a}}}_{z}ds)=E_{z}ds$

 

${\oint }_S\mathbf{\text{E}}\cdot d\mathbf{\text{s}}=2E_z{\int }_{A}ds=2E_{z}A={\rho }_{s}A/{ϵ}_0$

 

가우스의 법칙 적용

 

3. 구형의 전자구름에 발생되는 전기장 세기

 

$0\le R\le b$에서 $\rho =-{\rho }_0$, $R>b$ 에서 $\rho =0$

 

가우스 표면은 구 형태의 면을 사용하는 것이 적절하다.

 

$0\le R\le b$ 일 때

 

$$\oint \mathbf{\text{E}}\cdot d\mathbf{\text{s}}=E_R(4\pi R^2)=\frac{Q}{{ϵ}_0}$$

$$Q={\int }_v\rho dv=-{\rho }_0\frac{4\pi }{3}{R}^3$$

$$\mathbf{\text{E}}=-{\mathbf{\text{a}}}_R\frac{{\rho }_{0}R}{3{ϵ}_0}$$

 

$R\ge b$ 일 때

 

$$Q=-\frac{{\rho }_{0}4\pi b^3}{3},E_R(4\pi R^2)=\frac{Q}{{ϵ}_0}$$ 이므로 $$\mathbf{\text{E}}=-{\mathbf{\text{a}}}_R\frac{{\rho }_0{b}^3}{3{ϵ}_0{R}^2}$$

가우스의 법칙 적용

 

결과적으로, 전자구름 내부에서는 전기장 세기가 중심부로부터의 거리에 비례하고, 전자구름 밖에서 전기장  세기는 쿨롱의 법칙과 같이 생각할 수 있다.

 

출처-David K. Cheng.Field and Wave Electromagnetics