[Cheng의 전자기학] 정자기장의 기본 가정

 

 

 

전기장이 존재할 때, 정지하고 있는 매우 작은 시험전하 q가 받는 힘인 전기력은 다음과 같이 정의했다.

 

$${\mathbf{\text{F}}}_e=q\mathbf{\text{E}}(N)$$

 

시험전하가 움직이고 있을 때, 자기장에 의한 힘, 즉 자기력 또한 존재한다. 이 힘은 세 가지 특성이 있다.

 

1. 전하량에 비례

 

2. 시험전하의 움직이는 방향과 힘의 방향은 수직이고 자기장의 방향과도 수직

 

3. 힘의 크기는 일정 방향에 수직인 속도 성분의 크기에 비례

 

$${\mathbf{\text{F}}}_m=q\mathbf{\text{u}}\times \mathbf{\text{B}}(N)$$

 

u는 시험전하의 속도벡터이고 B는 자속밀도이다. 이를 바탕으로 총 전자기력은 전기력과 자기력의 합이다.

 

$$\mathbf{\text{F}}=q(\mathbf{\text{E}}+\mathbf{\text{u}}\times \mathbf{\text{B}})(N)$$

 

이 수식을 로렌츠 힘의 방정식이라고 한다.

 

 

정자기장의 기본 가정

 

 

자유공간 내에서 정자기장 B에 대한 기본 가정은 다음과 같다.

 

$$\mathrm{\nabla }\cdot \mathbf{\text{B}}=0$$

 

$$\mathrm{\nabla }\times \mathbf{\text{B}}={\mu }_0\mathbf{\text{J}}$$

 

${\mu }_0$ 는 자유공간 내의 투자율을 의미하고, J는 전류밀도이다. 모든 벡터장의 회전의 발산은 0 을 이용하여 두번째 가정을 전개할 수 있다.

 

$$\mathrm{\nabla }\cdot (\mathrm{\nabla }\times \mathbf{\text{B}})=\mathrm{\nabla }\cdot ({\mu }_0\mathbf{\text{J}})=0\to \mathrm{\nabla }\cdot \mathbf{\text{J}}=0$$

 

첫번째 정자기장 기본가정을 부피적분을 하고 발산 정리를 이용하면

 

$${\oint }_S\mathbf{\text{B}}\cdot d\mathbf{\text{s}}=0$$

 

이고, 유도된 수식을 정해보면, 자속선은 밖으로 나갔다 다시 그대로 돌아오고 있는, 닫혀 있는 상태를 의미한다. 예시로, 막대 자석을 생각했을 때, N극에서 S극으로 자기장이 향하고 있음을 알고 있다. 막대 자석을 매우 잘게 잘랐을 때에도 마찬가지이다. 따라서 자기장은 막대자석의 끝에서 끝으로 자석의 바깥 폐경로를 따른다.

 

막대자석의 자속선

 

두번째 정자기장의 기본가정의 양변을 적분하고 스토크스 정리를 사용해본다.

 

$${\oint }_S(\mathrm{\nabla }\times \mathbf{\text{B}})\cdot d\mathbf{\text{s}}={\mu }_0{\int }_S\mathbf{\text{J}}\cdot d\mathbf{\text{s}}\to {\oint }_C\mathbf{\text{B}}\cdot d\mathbf{\text{l}}={\mu }_{0}I$$

 

I는 표면 S를 통과하는 총 전류이고, C는 면 S를 구분하는 선이다. 위 수식은 암페어 법칙으로, 자속밀도의 순환은 폐경로에 둘러싸인 표면을 통해 흘러가는 총 전류에 투자율을 곱한 것과 같다는 의미이다.

 

 

벡터 자기장 포텐셜

 

 

$\mathrm{\nabla }\cdot \mathbf{\text{B}}=0$ 을 통해 자속밀도는 솔레노이드성이고

 

$$\mathbf{\text{B}}=\mathrm{\nabla }\times \mathbf{\text{A}}(T)$$

 

을 유도할 수 있다. A를 벡터 자기장 포텐셜이라고 한다. 

 

$$\mathrm{\nabla }\times \mathbf{\text{B}}=\mathrm{\nabla }\times \mathrm{\nabla }\times \mathbf{\text{A}}={\mu }_0\mathbf{\text{J}}$$

 

${\mathrm{\nabla }}^2\mathbf{\text{A}}=\mathrm{\nabla }(\mathrm{\nabla }\cdot \mathbf{\text{A}})-\mathrm{\nabla }\times \mathrm{\nabla }\times \mathbf{\text{A}}\to \mathrm{\nabla }\times \mathrm{\nabla }\times \mathbf{\text{A}}=\mathrm{\nabla }(\mathrm{\nabla }\cdot \mathbf{\text{A}})-{\mathrm{\nabla }}^2\mathbf{\text{A}}$ 으로 표현할 수 있다.

 

따라서 $\mathrm{\nabla }(\mathrm{\nabla }\cdot \mathbf{\text{A}})-{\mathrm{\nabla }}^2\mathbf{\text{A}}={\mu }_0\mathbf{\text{J}}$ 을 유도할 수 있고, $\mathrm{\nabla }\cdot \mathbf{\text{A}}=0$ 으로 놓으면 포아송 방정식과 같아진다.

 

$${\mathrm{\nabla }}^2\mathbf{\text{A}}=-{\mu }_0\mathbf{\text{J}}$$

 

$$\mathbf{\text{A}}=\frac{{\mu }_0}{4\pi }{\int }_{V^{\prime }}\frac{\mathbf{\text{J}}}{R}d{v}^{\prime }(Wb/m)$$

 

자속밀도를 면적에 대해 적분하면 해당하는 면적을 관통하는 자속$(\mathrm{\Phi })$ 이다.

 

$$\mathrm{\Phi }={\int }_S\mathbf{\text{B}}\cdot d\mathbf{\text{s}}={\int }_S(\mathrm{\nabla }\times \mathbf{\text{A}})\cdot d\mathbf{\text{s}}={\oint }_C\mathbf{\text{A}}\cdot d\mathbf{\text{l}}(Wb)$$

 

자속은 A로 유도할 수 있는데, A를 임의의 폐경로 C에 따라 선적분한 것이 그 경로의 면을 통과하는 자속과 같다는 것을 알 수 있다.

 

 

비오-사바르 법칙

 

 

$$\mathbf{\text{B}}={\oint }_{C^{\prime }}d\mathbf{\text{B}}(T)$$

$$d\mathbf{\text{B}}=\frac{{\mu }_{0}I}{4\pi }\frac{d\mathbf{\text{l'}}\times {\mathbf{\text{a}}}_R}{R^2}(T)ord\mathbf{\text{B}}=\frac{{\mu }_{0}I}{4\pi }\frac{d\mathbf{\text{l'}}\times \mathbf{\text{R}}}{R^3}(T)$$

 

비오-사바르 법칙은 위처럼 정리할 수 있다. 일반적으로 암페어 법칙은 대칭적이고, 전류 주위에 폐경로가 있어서 B의 크기가 경로를 따라 일정할 때 전류 I에 의해 발생하는 B의 크기를 구할 때 사용된다. 비오-사바르 법칙은 암페어 법칙을 적용하기 어려운 경우인 상황에 적용할 수 있다.

 

비오-사바르 법칙 예시

 

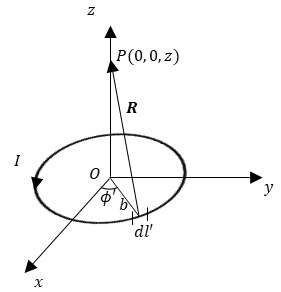
위의 그림처럼, 점 P에서의 자속밀도를 구하기 위해 비오-사바르 법칙을 이용한다.

 

$$1.d{\mathbf{\text{l}}}^{\prime }=a_{\varphi }bd{\varphi }^{\prime },\mathbf{\text{R}}={\mathbf{\text{a}}}_{z}z-{\mathbf{\text{a}}}_{r}b,R=(z^2+b^2{)}^{1/2}$$

 

$$2.d{\mathbf{\text{l}}}^{\prime }\times \mathbf{\text{R}}=a_{\varphi }bd{\varphi }^{\prime }\times ({\mathbf{\text{a}}}_{z}z-{\mathbf{\text{a}}}_{r}b)={\mathbf{\text{a}}}_{r}bzd{\varphi }^{\prime }+{\mathbf{\text{a}}}_z{b}^{2}d{\varphi }^{\prime }$$

$($원통형 좌표계에서 $a_{\varphi }\times a_z=a_r$, $a_{\varphi }\times a_r=-a_z$ $)$

 

$$3.\mathbf{\text{B}}=\frac{{\mu }_{0}I}{4\pi }{\int }_0^{2\pi }{\mathbf{\text{a}}}_z\frac{b^{2}d{\varphi }^{\prime }}{(z^2+b^2{)}^{3/2}}={\mathbf{\text{a}}}_z\frac{{\mu }_{0}I{b}^2}{2(z^2+b^2{)}^{3/2}}$$

 

 

출처-David K. Cheng.Field and Wave Electromagnetics