포아송 방정식과 라플라스 방정식
정전기장에 관한 미분 방정식은 E와 D로 나타낼 수 있다.
$$ \nabla \cdot \textbf{D} = \rho $$
$$ \nabla \times \textbf{E} = 0 $$
2번째 수식은 정전기장 조건에서 $ \textbf{E}=-\nabla V $ 로 표현할 수 있고 $\textbf{D} = \epsilon \textbf{E}$ 로 표현할 수 있어서 포아송 방정식을 만들 수 있다.
$$ \nabla \cdot (\epsilon (- \nabla V )) = \rho $$
$$ \nabla^2 V = -\frac{\rho}{\epsilon} $$
포아송 방정식에서 자유전하 없이 $ \rho=0 $인 단순 매질 내의 한 점을 나타내면 라플라스 방정식으로 바뀐다.
$$ \nabla^2 V = 0 $$
예시로 두 평판 커패시터가 거리 $d$만큼 떨어진 채로 전위차가 존재할 때 거리에 따라 전기장이 달라진다.

$x$축과 $z$축은 영향이 없고 자유전하가 존재하지 않기 때문에 라플라스 방정식을 사용할 수 있다.
$$ \frac{d^2 V}{d y^2}=0 $$
위 식을 $y$에 대해 두 번 적분하면 두 개의 적분상수를 얻을 수 있고 두 개의 경계 조건으로 적분상수를 모두 구할 수 있다.
$$ V = C_1 y + C_2 $$
경계 조건은 $y=0$ 일 때 전위는 0이고 $y = d$ 일 때 전위는 $V_0$ 이다.
$$V = \frac{V_0}{d} y$$
정전기장에서 $\textbf{E} = -\nabla V$ 이고 전기장의 방향은 +에서 -로 $-y$ 방향이다.
$$ \textbf{E} = -a_y \frac{dV}{dy} = -a_y \frac{V_0}{d} $$
도체의 경계 부분에서는 전기장의 수직 성분을 이용하여 전하 밀도를 구할 수 있다. 따라서 윗판과 아랫판 각각 전하 밀도를 알 수 있다.
$$ \rho_{top} = \frac{\epsilon V_0}{d} $$
$$ \rho_{bottom} = -\frac{\epsilon V_0}{d} $$
두 전하밀도는 자유전하가 없는 정전기장이므로 내부 전하가 존재하지 않고 모두 표면에 전하가 존재하기 때문에 면전하밀도이다.
영상법
영상법은 포아송 방정식이나 라플라스 방정식을 사용하여 직접 풀 때 경계 조건을 사용하기 어려운 경우에서 사용된다. 주어진 전하 말고 새로운 전하를 생각해내서 대칭적으로 위치시켜 주어진 상황을 쉽게 생각한다.

그림처럼 빨간색 선이 접지된 도체판이고 점전하 $Q$가 있다. 먼저 $x$축에 대칭으로 $-Q$가 영상전하로 존재한다면 $x$축에 놓인 접지된 도체판의 전위는 0이다. 마찬가지로, $y$축에 대칭으로 $-Q$가 영상전하로 존재한다면 $y$축에 놓진 접지된 도체판의 전위는 0이다. 이제 두 도체판의 전위가 모두 0을 만족하려면 점전하 $Q$와 원점대칭에 $+Q$가 영상전하로 존재해야 한다.

영상법을 이용해 서로 수직인 도체판 대신에 영상 전하들로 생각하여 양전하 $Q$에 가해지는 힘을 구할 수 있다.
$$ \textbf{F} _{12} = q_2\textbf{E} _{12} = a_R \frac{q_1 q_2}{4\pi \epsilon_0 R^2} $$
다음 두 점전하 사이를 쿨롱의 법칙을 이용하면 힘을 구할 수 있다.
$$ \textbf{F}_1 = -a_y \frac{Q^2}{4\pi \epsilon_0 (2d_2)^2} $$
$$ \textbf{F}_2 = -a_x \frac{Q^2}{4\pi \epsilon_0 (2d_1)^2} $$
$$ \textbf{F}_3 = \frac{Q^2}{4\pi \epsilon_0 [(2d_1)^2 + (2d_2)^2]^{3/2}}(a_x 2d_1 + a_y 2d_2) $$
서로 직각인 두 도체판 근처에 있는 양전하 $Q$에 가해지는 힘은 위에 구한 세 힘의 벡터 합이다.
경계치 문제
처음에 나왔던 라플라스 방정식의 해를 구하기 위해 변수분리법을 적용한다.
$$ V(x,y,z) = X(x)Y(y)Z(z) $$
위 식처럼 변수분리법을 적용한 후 라플라스 방정식에 대입한다.
$$ Y(y)Z(z) \frac{d^2 X(x)}{dx^2} + X(x)Z(z) \frac{d^2 Y(y)}{dy^2} + X(x)Y(x) \frac{d^2 Z(z)}{dz^2} = 0 $$
$$ \frac{1}{X(x)} \frac{d^2 X(x)}{dx^2} + \frac{1}{Y(y)} \frac{d^2 Y(y)}{dy^2} + \frac{1}{Z(z)} \frac{d^2 Z(z)}{dz^2} = 0 $$
따라서 세 항이 모두 상수여야만 합이 0임을 생각할 수 있다.
$$ \frac{1}{dx} \left [ \frac{1}{X(x)} \frac{d^2 X(x)}{dx^2} \right ] = 0 $$
상수를 미분하면 0이므로 위처럼 생각할 수 있고, 다시 적분을 하게 되면 적분상수를 얻는다.
$$ \frac{1}{X(x)} \frac{d^2 X(x)}{dx^2} = -k_x ^2$$
$-k_x ^2$ 을 적분상수로 한 것은 임의로 정한 것이다.
$$ \frac{d^2 X(x)}{dx^2} + k_x ^2 X(x) = 0 $$
$y,\, z$도 똑같이 구할 수 있고 $ k_x ^2 + k_y ^2 + k_z ^2 =0$ 를 만족한다.
| $k_x ^2$ | $k_x$ | $X(x)$ | 지수 형태의 $X(x)$ |
| 0 | 0 | $A_0 x + B_0$ | |
| $+$ | $k$ | $A_1 \sin kx + B_1 \cos kx$ | $C_1 e^{jkx}+ D_1 e^{-jkx}$ |
| $-$ | $jk$ | $A_1 \sinh kx + B_1 \cosh kx$ | $C_2 e^{kx} + D_2 e^{-kx}$ |
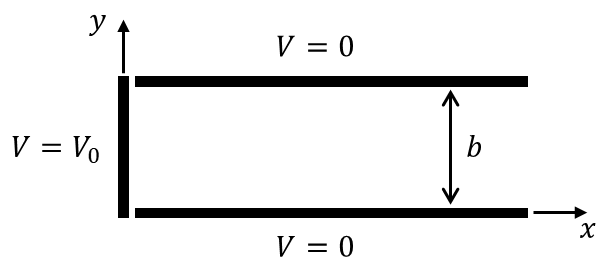
그림과 같은 예시가 있을 때, $z$축은 고려하지 않고 경계조건을 생각한다.
$$ V(x,y,z) \rightarrow V(x,y) $$
$x$축 방향 경계조건 :
$$ V(0,y) = V_0 $$
$$ V(\infty, y) = 0 $$
$y$축 방향 경계조건 :
$$ V(x,0) = 0 $$
$$ V(x,b) = 0 $$
$k_z=0$ 을 만족하기 때문에 $ Z(z) = B_0 $ 으로 상수값을 갖는다.
$$ k_x^2 + k_y^2 = 0 \quad \rightarrow \quad k_y^2 = -k_x^2 = k^2 $$
여기서 $k$는 실수이다. 위에 표현된 값으로 $k_x=jk$ 로 허수, $k_y = k$ 로 실수를 나타낸다. 위에 나타난 표를 이용해서 $X(x)$와 $Y(y)$ 를 유도할 수 있다. 여기서 경계조건 일부가 사용된다.
$$ X(x) = D_2 e^{-kx} $$
$x \rightarrow \infty$ 일 때 $V=0$ 이므로 $C_2=0$ 을 만족해야 하고,
$$ Y(y) = A_1 \sin ky $$
$y=0$ 일 때 $V=0$ 이므로 $B_1=0$ 을 만족한다.
$$ V_n (x,y) = (B_0 D_2 A_1)e^{-kx} \sin ky = C_n e^{-kx} \sin ky $$
$X(x)$ 는 물리적으로 $x$축에서 멀어질수록 세기가 감소하고, $Y(y)$ 는 $y$축 방향으로 사인파 형태로 크기가 나타난다. 상수 $C_n$ 은 상수들의 곱을 표현한다. 이제 남은 경계조건을 만족해야 한다.
먼저, 경계조건 $V(x,b)=0$ 을 고려한다.
$$C_n e^{-kx} \sin ky = 0 \rightarrow \sin kb = 0 \rightarrow kb = n \pi \rightarrow k= \frac{n \pi}{b} \quad n = 1,2,3,\cdots$$
남은 경계조건 $V(0,y)=V_0$ 을 고려한다. 라플라스 방정식은 선형 편미분 방정식이므로 중첩도 해가 된다.
$$ V(0,y) = \sum_{n=1}^{infty} V_n (0,y) = \sum_{n=1}^{\infty} C_n \sin \frac{n \pi}{b} y = V_0 \quad 0<y<b $$
위 식으로 확실하게 $x=0$에서 $0<y<d$는 무수히 많은 사인파들의 합으로, 주기적인 구형파를 생성하는 것을 알 수 있다.
이제 계수 $C_n$을 구하기 위해서 양변에 $\sin \frac{m\pi}{b}$ 을 곱한 후 0부터 $b$까지 적분을 한다. 이렇게 하는 이유는 계수를 구하기 위해 기저 함수인 $\sin$ 함수의 직교 성질, 즉 $m \neq n$인 경우와 $m=n$인 경우를 생각해야 한다.
우변을 먼저 계산한다.
$$ \int_0^b V_0 \sin \frac{m\pi}{b} y dy = \frac{2bV_0}{m\pi} \; (m\, is\, odd) \quad or \quad 0 \; (m\, is\, even) $$
좌변을 계산한다.
$$ \int_0^b C_n \sin \frac{n\pi}{b}y \, \sin \frac{m \pi}{b}y \,dy = \frac{C_n}{2}b \; (m=n) \quad or \quad 0 \; (m \neq n) $$
따라서 $n$이 홀수라면 $C_n=\frac{4V_0}{n\pi}$이고 $n$이 짝수라면 $C_n=0$이다.
마지막으로, 전위를 다시 정리한다.
$$ V(x,y)=\frac{4V_0}{\pi} \sum_{n=odd}^{\infty} \frac{1}{n}e^{-n\pi x/b} \sin \frac{n\pi}{b}\,y \quad n=1,3,5,\cdots, \; x>0, \; 0<y<b$$
출처-David K. Cheng.Field and Wave Electromagnetics
'전자기학' 카테고리의 다른 글
| [Cheng의 전자기학] 정자기장의 기본 가정 (0) | 2025.03.02 |
|---|---|
| [Cheng의 전자기학] 정전기장의 경계 조건과 정전용량 (0) | 2025.02.16 |
| [Cheng의 전자기학] 전위와 매질 내에서의 전기장 (0) | 2025.02.09 |
| [Cheng의 전자기학] 가우스의 법칙 (0) | 2025.02.02 |
| [Cheng의 전자기학] 벡터장 정리 (0) | 2025.01.26 |