[Cheng의 전자기학] 정전기장 문제의 해

 

 

 

포아송 방정식과 라플라스 방정식

 

 

정전기장에 관한 미분 방정식은 E와 D로 나타낼 수 있다.

 

$$\mathrm{\nabla }\cdot \mathbf{\text{D}}=\rho$$

 

$$\mathrm{\nabla }\times \mathbf{\text{E}}=0$$

 

2번째 수식은 정전기장 조건에서 $\mathbf{\text{E}}=-\mathrm{\nabla }V$ 로 표현할 수 있고 $\mathbf{\text{D}}=ϵ\mathbf{\text{E}}$ 로 표현할 수 있어서 포아송 방정식을 만들 수 있다.

 

$$\mathrm{\nabla }\cdot (ϵ(-\mathrm{\nabla }V))=\rho$$

$${\mathrm{\nabla }}^{2}V=-\frac{\rho }{ϵ}$$

 

포아송 방정식에서 자유전하 없이 $\rho =0$인 단순 매질 내의 한 점을 나타내면 라플라스 방정식으로 바뀐다.

 

$${\mathrm{\nabla }}^{2}V=0$$

 

예시로 두 평판 커패시터가 거리 $d$만큼 떨어진 채로 전위차가 존재할 때 거리에 따라 전기장이 달라진다.

 

평판 커패시터

 

$x$축과 $z$축은 영향이 없고 자유전하가 존재하지 않기 때문에 라플라스 방정식을 사용할 수 있다.

 

$$\frac{d^{2}V}{d{y}^2}=0$$

 

위 식을 $y$에 대해 두 번 적분하면 두 개의 적분상수를 얻을 수 있고 두 개의 경계 조건으로 적분상수를 모두 구할 수 있다.

 

$$V=C_{1}y+C_2$$

 

경계 조건은 $y=0$ 일 때 전위는 0이고 $y=d$ 일 때 전위는 $V_0$ 이다.

 

$$V=\frac{V_0}{d}y$$

 

정전기장에서 $\mathbf{\text{E}}=-\mathrm{\nabla }V$ 이고 전기장의 방향은 +에서 -로 $-y$ 방향이다.

 

$$\mathbf{\text{E}}=-a_y\frac{dV}{dy}=-a_y\frac{V_0}{d}$$

 

도체의 경계 부분에서는 전기장의 수직 성분을 이용하여 전하 밀도를 구할 수 있다. 따라서 윗판과 아랫판 각각 전하 밀도를 알 수 있다.

 

$${\rho }_{top}=\frac{ϵV_0}{d}$$

 

$${\rho }_{bottom}=-\frac{ϵV_0}{d}$$

 

두 전하밀도는 자유전하가 없는 정전기장이므로 내부 전하가 존재하지 않고 모두 표면에 전하가 존재하기 때문에 면전하밀도이다.

 

 

영상법

 

 

영상법은 포아송 방정식이나 라플라스 방정식을 사용하여 직접 풀 때 경계 조건을 사용하기 어려운 경우에서 사용된다. 주어진 전하 말고 새로운 전하를 생각해내서 대칭적으로 위치시켜 주어진 상황을 쉽게 생각한다.

 

 

양전하와 도체판

 

 

그림처럼 빨간색 선이 접지된 도체판이고 점전하 $Q$가 있다. 먼저 $x$축에 대칭으로 $-Q$가 영상전하로 존재한다면 $x$축에 놓인 접지된 도체판의 전위는 0이다. 마찬가지로, $y$축에 대칭으로 $-Q$가 영상전하로 존재한다면 $y$축에 놓진 접지된 도체판의 전위는 0이다. 이제 두 도체판의 전위가 모두 0을 만족하려면 점전하 $Q$와 원점대칭에 $+Q$가 영상전하로 존재해야 한다.

 

 

전하 Q에 가해지는 힘

 

 

영상법을 이용해 서로 수직인 도체판 대신에 영상 전하들로 생각하여 양전하 $Q$에 가해지는 힘을 구할 수 있다.

 

$${\mathbf{\text{F}}}_{12}=q_2{\mathbf{\text{E}}}_{12}=a_R\frac{q_1{q}_2}{4\pi {ϵ}_0{R}^2}$$

 

다음 두 점전하 사이를 쿨롱의 법칙을 이용하면 힘을 구할 수 있다.

 

$${\mathbf{\text{F}}}_1=-a_y\frac{Q^2}{4\pi {ϵ}_0(2d_2{)}^2}$$

 

$${\mathbf{\text{F}}}_2=-a_x\frac{Q^2}{4\pi {ϵ}_0(2d_1{)}^2}$$

 

$${\mathbf{\text{F}}}_3=\frac{Q^2}{4\pi {ϵ}_0[(2d_1{)}^2+(2d_2{)}^2{]}^{3/2}}(a_{x}2d_1+a_{y}2d_2)$$

 

서로 직각인 두 도체판 근처에 있는 양전하 $Q$에 가해지는 힘은 위에 구한 세 힘의 벡터 합이다.

 

 

경계치 문제

 

 

처음에 나왔던 라플라스 방정식의 해를 구하기 위해 변수분리법을 적용한다.

 

$$V(x,y,z)=X(x)Y(y)Z(z)$$

 

위 식처럼 변수분리법을 적용한 후 라플라스 방정식에 대입한다.

 

$$Y(y)Z(z)\frac{d^{2}X(x)}{d{x}^2}+X(x)Z(z)\frac{d^{2}Y(y)}{d{y}^2}+X(x)Y(x)\frac{d^{2}Z(z)}{d{z}^2}=0$$

 

$$\frac{1}{X(x)}\frac{d^{2}X(x)}{d{x}^2}+\frac{1}{Y(y)}\frac{d^{2}Y(y)}{d{y}^2}+\frac{1}{Z(z)}\frac{d^{2}Z(z)}{d{z}^2}=0$$

 

따라서 세 항이 모두 상수여야만 합이 0임을 생각할 수 있다.

 

$$\frac{1}{dx}\left[\frac{1}{X(x)}\frac{d^{2}X(x)}{d{x}^2}\right]=0$$

 

상수를 미분하면 0이므로 위처럼 생각할 수 있고, 다시 적분을 하게 되면 적분상수를 얻는다.

 

$$\frac{1}{X(x)}\frac{d^{2}X(x)}{d{x}^2}=-k_x^2$$

 

$-k_x^2$ 을 적분상수로 한 것은 임의로 정한 것이다.

 

$$\frac{d^{2}X(x)}{d{x}^2}+k_x^{2}X(x)=0$$

 

$y,z$도 똑같이 구할 수 있고 $k_x^2+k_y^2+k_z^2=0$ 를 만족한다.

 

$k_x^2$	$k_x$	$X(x)$	지수 형태의 $X(x)$
0	0	$A_{0}x+B_0$
$+$	$k$	$A_1\sin kx+B_1\cos kx$	$C_1{e}^{jkx}+D_1{e}^{-jkx}$
$-$	$jk$	$A_1\sinh kx+B_1\cosh kx$	$C_2{e}^{kx}+D_2{e}^{-kx}$

 

 

x축으로 무한한 길이의 접지된 도체 평면과 y축으로 길이가 b인 전위가 존재하는 도체 평면

 

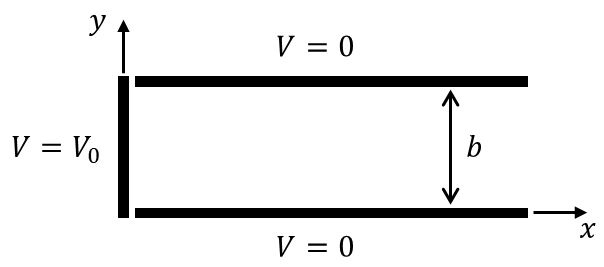
그림과 같은 예시가 있을 때, $z$축은 고려하지 않고 경계조건을 생각한다.

 

$$V(x,y,z)\to V(x,y)$$

 

$x$축 방향 경계조건 :

$$V(0,y)=V_0$$

 

$$V(\mathrm{\infty },y)=0$$

 

$y$축 방향 경계조건 :

 

$$V(x,0)=0$$

 

$$V(x,b)=0$$

 

$k_z=0$ 을 만족하기 때문에 $Z(z)=B_0$ 으로 상수값을 갖는다.

 

$$k_x^2+k_y^2=0\to k_y^2=-k_x^2=k^2$$

 

여기서 $k$는 실수이다. 위에 표현된 값으로 $k_x=jk$ 로 허수, $k_y=k$ 로 실수를 나타낸다. 위에 나타난 표를 이용해서 $X(x)$와 $Y(y)$ 를 유도할 수 있다. 여기서 경계조건 일부가 사용된다.

 

$$X(x)=D_2{e}^{-kx}$$

 

$x\to \mathrm{\infty }$ 일 때 $V=0$ 이므로 $C_2=0$ 을 만족해야 하고,

 

$$Y(y)=A_1\sin ky$$

 

$y=0$ 일 때 $V=0$ 이므로 $B_1=0$ 을 만족한다.

 

$$V_n(x,y)=(B_0{D}_2{A}_1)e^{-kx}\sin ky=C_n{e}^{-kx}\sin ky$$

 

$X(x)$ 는 물리적으로 $x$축에서 멀어질수록 세기가 감소하고, $Y(y)$ 는 $y$축 방향으로 사인파 형태로 크기가 나타난다. 상수 $C_n$ 은 상수들의 곱을 표현한다. 이제 남은 경계조건을 만족해야 한다.

 

먼저, 경계조건 $V(x,b)=0$ 을 고려한다.

 

$$C_n{e}^{-kx}\sin ky=0\to \sin kb=0\to kb=n\pi \to k=\frac{n\pi }{b}n=1,2,3,\cdots$$

 

남은 경계조건 $V(0,y)=V_0$ 을 고려한다. 라플라스 방정식은 선형 편미분 방정식이므로 중첩도 해가 된다.

 

$$V(0,y)=\sum _{n=1}^{infty}{V}_n(0,y)=\sum _{n=1}^{\mathrm{\infty }}{C}_n\sin \frac{n\pi }{b}y=V_{0}0<y<b$$

 

위 식으로 확실하게 $x=0$에서 $0<y<d$는 무수히 많은 사인파들의 합으로, 주기적인 구형파를 생성하는 것을 알 수 있다.

 

이제 계수 $C_n$을 구하기 위해서 양변에 $\sin \frac{m\pi }{b}$ 을 곱한 후 0부터 $b$까지 적분을 한다. 이렇게 하는 이유는 계수를 구하기 위해 기저 함수인 $\sin$ 함수의 직교 성질, 즉 $m\ne n$인 경우와 $m=n$인 경우를 생각해야 한다.

 

우변을 먼저 계산한다.

 

$${\int }_0^b{V}_0\sin \frac{m\pi }{b}ydy=\frac{2b{V}_0}{m\pi }(misodd)or0(miseven)$$

 

좌변을 계산한다.

 

$${\int }_0^b{C}_n\sin \frac{n\pi }{b}y\sin \frac{m\pi }{b}ydy=\frac{C_n}{2}b(m=n)or0(m\ne n)$$

 

따라서 $n$이 홀수라면 $C_n=\frac{4V_0}{n\pi }$이고 $n$이 짝수라면 $C_n=0$이다.

 

마지막으로, 전위를 다시 정리한다.

 

$$V(x,y)=\frac{4V_0}{\pi }\sum _{n=odd}^{\mathrm{\infty }}\frac{1}{n}{e}^{-n\pi x/b}\sin \frac{n\pi }{b}yn=1,3,5,\cdots ,x>0,0<y<b$$

 

 

출처-David K. Cheng.Field and Wave Electromagnetics